Record(2)
非交互式knn隐私保护分类器
一、用途
对存储在云中的私有数据库运行查询
二、基本概念
1、kNN分类器
1)特点:无监督机器学习
2)分类:(通常采用欧氏距离)
未加权(选择距离最小的k个实例)
加权(距离的倒数作为k个邻居中每个邻居的投票权重)
2、保序加密
功能:密文保持明文的数字顺序
加密原理:
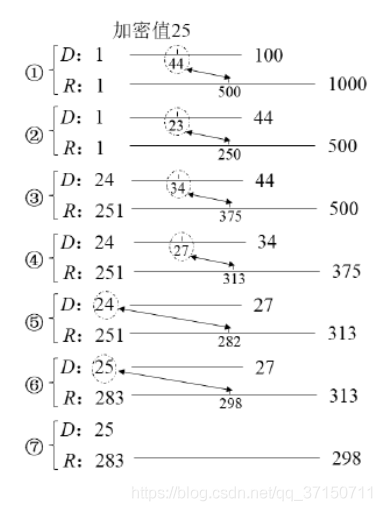
解密原理:反向查表
参考文章:密码学——保序加密算法
import csv
import random
import numpy as np
key_table = "BCLO09.csv"
def HGD(D, R):
len_D = len(D)
len_R = len(R)
y = int(len_R / 2)
x = np.random.hypergeometric(len_D, len_R, y, size=1)
a = x[0]
if x[0] >= len_D:
a = len_D - 1
return D[a]
def writeCsv(path, data, modle): #传入变量csv文件的路径和要写入的数据
with open(path,modle,newline="") as f: # 以写入的方式打开文件,newline="" 可以让数据不隔行写入
writer_csv=csv.writer(f) #调用csv的writer方法往文件里面写入数据,并赋值给writer_scv变量
writer_csv.writerow(data) #把数据循环写入到writer_csv变量中
#读取csv文件
def readCsv(path): #传入变量csv文件的路径
list_one=[] #定义一个空列表
with open(path,"r") as f: #以只读的方式打开文件
read_scv=csv.reader(f) #调用csv的reader方法读取文件并赋值给read_scv变量
for i in read_scv:
list_one.append(i) #将读取到的数据追加到list列表里面
return list_one #返回列表数据
def key_tableIsContain(param):
list_one = readCsv(key_table)
if len(list_one) == 0:
return 0, 0
flag = 0
for i in range(len(list_one)):
if str(int(param)) == list_one[i][0]:
flag = 1
return 1, int(list_one[i][1])
if flag != 1:
return 0, 0
def Enc2(key_table, D, R, m):
_D = D
_R = R
M = max(D) - min(D) + 1
N = max(R) - min(R) + 1
center = int((max(R) + min(R)) / 2)
iscontain, values = key_tableIsContain(center)
if iscontain == 1:
c = values #记录D中的抽样值
x = values
else:
x = HGD(D, R)
a = []
a.append(center)
a.append(x)
writeCsv(key_table, a ,"a")
print("区间是D[%d, %d]" % (min(_D), max(_D)))
print("区间是R[%d, %d]" % (min(_R), max(_R)))
if M == 1:
print(m)
print("区间是R[%d, %d]" % (min(_R), max(_R)))
# return random.randint(min(R), max(R))
return str(m) + " " + str(min(R)) + " " + str(max(R))
if M == 2:
print(m)
if min(D) == m:
print("最后的区间是R(%d, %d]" % (min(_R), center))
return str(m) + " " + str(min(R)) + " " + str(center)
else:
print("最后的区间是R(%d, %d]\n" % (center, max(_R)))
return str(m) + " " + str(center) + " " + str(max(R))
# return random.randint(min(R), max(R))
if m <= x: #左边
D = []
for i in range(min(_D), x + 1):
D.append(i)
R = []
for j in range(min(_R), center + 1):
R.append(j)
else: #右边
D = []
for i in range(x + 1, max(_D) + 1):
D.append(i)
R = []
for j in range(center + 1, max(_R) + 1):
R.append(j)
print("D[%d, %d] 抽样值:%d"%(min(_D), max(_D), x))
print("R[%d, %d] 中间值:%d \n" % (min(_R), max(_R), center))
return Enc2(key_table, D, R, m)
def Dnc2(key_table, D, R, m):
_D = D
_R = R
M = max(D) - min(D) + 1
N = max(R) - min(R) + 1
center = int((max(R) + min(R)) / 2)
print("区间是D[%d, %d]" % (min(_D), max(_D)))
print("区间是R[%d, %d]" % (min(_R), max(_R)))
if M == 1:
print(m)
print("明文是:%d\n区间是R[%d, %d]" % (min(D), min(_R), max(_R)))
return random.randint(min(R), max(R))
if M == 2:
if m <= center:
print("明文是:%d\n最后的区间是R(%d, %d]" % (min(D), min(_R), center))
else:
print("明文是:%d\n最后的区间是R[%d, %d)\n" % (max(D), center, max(_R)))
return random.randint(min(R), max(R))
iscontain, values = key_tableIsContain(center)
if iscontain == 1:
c = values # 记录D中的抽样值
x = values
else:
print("可能解密错误!")
return
x = HGD(D, R)
a = []
a.append(center)
a.append(x)
# writeCsv(key_table, a, "a")
if m <= center: # 左边
D = []
for i in range(min(_D), x + 1):
D.append(i)
R = []
for j in range(min(_R), center + 1):
R.append(j)
else: # 右边
D = []
for i in range(x + 1, max(_D) + 1):
D.append(i)
R = []
for j in range(center + 1, max(_R) + 1):
R.append(j)
return Dnc2(key_table, D, R, m)
if __name__ == '__main__':
# searchContentList = searchContent()
# print(searchContentList)
# Back()
while (1):
print("=================\n"
"\t1、加密\n"
"\t2、解密\n"
"\t3、循环加密\n"
"=================")
flag = input("请输入你要操作的编号:")
if flag == "1":
D = []
for i in range(100):
D.append(i + 1)
R = []
for i in range(1000):
R.append(i + 1)
m = input("请输入你要加密的数字")
Enc2(key_table, D, R, int(m))
if flag == "2":
D = []
for i in range(100):
D.append(i + 1)
R = []
for i in range(1000):
R.append(i + 1)
m = input("请输入你要解密的数字")
Dnc2(key_table, D, R, int(m))
if flag == "3":
D = []
result = []
for i in range(100):
D.append(i + 1)
R = []
for i in range(1000):
R.append(i + 1)
for i in range(100):
result.append(Enc2(key_table, D, R, int(i + 1)))
for c in range(len(result)):
print(result[c])
3、同态加密
功能:经过同态加密的数据进行处理得到的结果与用相同方法处理未加密得到的结果相同
方案一

方案二
参考文章:Paillier cryptosystem(Paillier 密码系统)

三、实验结果
- 明文版本的k-NN比加密版本的速度快15倍。
- 该隐私保护方法不会丢失显著的分类准确性
- 该方案可能容易受到基于频率分析的推理攻击
改进方法:数据混淆和扰动技术 - 执行时间随实例数量呈线性增长
- 计算每个距离的时间也随相关向量的维数线性增长
四、其他方案
- 各方分别持有同一组数据的不同属性,分别计算各自分区内实例与查询向量的距离,加同态加密方案和随机扰动技术把这些距离结合起来找到k个最近邻(Zhan等,2005)(交互)
- 几个数据所有者每个人都有一个私有数据库,新实例的分类由每个用户在自己的数据库中执行,根据每个数据库的k个最近邻对实例进行分类(Xiong等人,2006;Xiong等人,2007)(交互)
- 三种保护数据隐私的方法来找到k个最邻近的邻居(Choi等,2014)(不执行分类问题)(交互)
- 数据所有者对数据进行加密并将其发送到云,其他用户可以提交查询向量以保持隐私的方式获得最近的邻居。(Zhu等,2013)(不执行分类问题)(交互)
- 据所有者加密数据并将其提交给第一台服务器,然后将密钥发送给第二台服务器,向第一台服务器发送查询向量,第一与第二服务器运行分布式交互式协议,最后第一服务器返回k个最近的邻居(Elmehdwi等,2014)(共谋)
- 该方案保留了一种特殊类型的标量积,允许在不需要交互过程的情况下找到k个最接近的向量。服务器通过计算加密向量的内积来计算数据集向量之间的内积,确定更接近查询向量的向量。(Wong et al.,2009)(不执行分类问题)
五、疑问
- 对于kNN,为什么要采用保序+同态方案?为什么不能仅使用同态?
- 在Linux下运行是否是因为该方案将应用于云环境?

